Recherche sur le chaos

La théorie du chaos ou théorie du chaos fait référence à une branche non clairement circonscrite de la dynamique non linéaire et des systèmes dynamiques , à laquelle de la physique mathématique ou des mathématiques appliquées est attribuée.

Essentiellement, il traite des ordres dans des systèmes dynamiques spéciaux, dont le développement au fil du temps semble imprévisible , bien que les équations sous-jacentes soient déterministes . Ce comportement est connu sous le nom de chaos déterministe et se produit lorsque les systèmes sont sensibles aux conditions initiales : des répétitions très légèrement différentes d'une expérience peuvent conduire à des résultats de mesure très différents dans le comportement à long terme (la théorie du chaos ne dit pas que des conditions initiales identiques conduiraient à des résultats différents). Les systèmes dynamiques chaotiques ne sont pas linéaires .

A titre d'exemple introductif, on se réfère souvent au pendule magnétique ou au double pendule . D'autres exemples sont l' effet papillon dans les conditions météorologiques , les turbulences , les cycles économiques , certains processus de formation de modèles tels que l' érosion , la formation d' embouteillages , les réseaux de neurones et les lasers .

La recherche sur le chaos s'appuie, entre autres, sur les travaux d' Henri Poincaré , Edward N. Lorenz , Benoît Mandelbrot et Mitchell Feigenbaum . Les phénomènes présentés ici correspondent au consensus minimal sur ce qui fait thématiquement partie de la recherche sur le chaos.

Basiques

Classification du comportement d'un pendule magnétique sur trois aimants; chaque point correspond à un point de départ du mouvement pendulaire. La couleur caractérise l'aimant sur lequel le pendule s'arrête. Plus la couleur est claire, plus elle sera précoce. Les trois points les plus brillants marquent donc les positions des aimants.

La théorie du chaos décrit le comportement temporel des systèmes à dynamique chaotique déterministe. Si l'on essaie de répéter les expériences à l'identique, cela n'est pas possible en pratique, car en raison d' imprécisions de mesure inévitables - et en raison du bruit  - la situation initiale ne peut pas être rétablie à l'identique. Si un système est chaotique de manière déterministe, le système peut, après un temps suffisamment long, conduire à des états finaux ou des résultats de mesure significativement différents malgré des situations initiales expérimentalement presque identiques (ou, dans la mesure du possible, identiques).

C'est ce qu'on appelle la "dépendance sensible aux conditions initiales". De tels systèmes peuvent être simulés sur ordinateur et ces simulations peuvent en principe être répétées à l'identique ou avec de faibles écarts. La sensibilité de la condition initiale se présente ici sous la forme que si on z. B. la précision de la condition de départ change légèrement, le résultat de la simulation est fondamentalement modifié. Ceci est dû au fait que les trajectoires arbitrairement proches au début n'ont plus cette propriété à la fin de la simulation. (Mathématiquement: la continuité de la cartographie est donnée pour les petits temps, mais plus dans les limes des grands temps.)

Dans l'illustration ci-contre, les conditions initiales caractérisées par des points dans le plan sont colorées différemment selon l'état final. D'une part il y a des zones (ici: dans la zone externe) qui forment des structures fractales , bien que les conditions initiales associées avec différents états finaux soient arbitrairement proches et d'autre part il y a des zones déterministes (ici: plus à l'intérieur), c'est-à-dire des zones dans lequel les conditions initiales voisines ont toutes le même état final.

Contrairement à l'utilisation familière du terme chaos, la théorie du chaos ne traite pas des systèmes soumis au hasard (c'est-à-dire des systèmes stochastiques ), mais des systèmes dynamiques qui peuvent être décrits mathématiquement et qui en principe se comportent de manière déterministe. En outre, la théorie du chaos doit être distinguée de la théorie des systèmes complexes , car des systèmes très simples peuvent également montrer un comportement chaotique.

définition

Un système dynamique est appelé chaotique s'il existe un ensemble -invariant , i.e. H. pour chaque et chaque est , qui: ${\ displaystyle (T, X, f)}$${\ displaystyle f}$${\ displaystyle Y \ subseteq X}$${\ displaystyle t \ in T}$${\ displaystyle y \ in Y}$${\ Displaystyle f (t, y) \ in Y}$

1. ${\ displaystyle f}$a une dépendance sensible des conditions initiales .${\ displaystyle Y}$
2. ${\ displaystyle f}$est topologiquement transitif à : Pour tous les ensembles ouverts avec il existe tel que .${\ displaystyle Y}$
   ${\ displaystyle U, V \ subseteq X}$${\ displaystyle U \ cap Y \ neq \ emptyset \ neq V \ cap Y}$${\ displaystyle t> 0}$${\ displaystyle f (t, U) \ cap V \ neq \ emptyset}$
3. Les périodiques orbites de sont proches de .${\ displaystyle f}$${\ displaystyle Y}$

Limites de la prévisibilité

Si le comportement est chaotique, même le moindre changement des valeurs initiales conduit à un comportement complètement différent après une période de temps finie, qui dépend du système considéré (dépendance sensible aux conditions initiales). Cela montre un comportement imprévisible qui semble se développer de manière irrégulière au fil du temps. Le comportement du système à certaines valeurs initiales (ou à leur voisinage) peut être complètement régulier s'il est par ex. B. est une orbite périodique.

Cependant, même le plus petit changement des valeurs initiales peut conduire à un comportement complètement différent après un temps suffisamment long, qui peut également apparaître complètement irrégulier. Afin de pouvoir calculer le comportement du système pour un certain temps futur, il faudrait donc que les conditions initiales soient connues et calculées avec une précision infiniment précise, ce qui est pratiquement impossible. Bien que de tels systèmes soient également déterministes et puissent donc être déterminés en principe, les prévisions pratiques ne sont donc possibles que pour des périodes de temps plus ou moins courtes.

Ce phénomène est également devenu connu du public sous l' effet de papillon d' accroche , selon lequel même le faible battement des ailes d'un papillon très éloigné peut conduire à une évolution différente de la météo à grande échelle à long terme.

Théorie quantique, déterminisme et flou

Dans ce qui suit, la détermination de la mécanique quantique (et ses limites par le principe d'incertitude de Heisenberg ) est expliquée sur la base de l' interprétation de Copenhague . Pour toutes les autres interprétations de la mécanique quantique , par exemple la théorie de De Broglie-Bohm , la section suivante n'est que partiellement correcte.

Alors que la prévisibilité de systèmes complexes réels au sens de la physique classique échoue parce que les conditions initiales ne sont pratiquement jamais des mesures complètement exactes, la prise en compte des découvertes de la physique quantique montre que leur comportement n'est en principe pas déterminé. Le principe d'incertitude de Heisenberg dit que la position et l'élan d'un objet ne peuvent pas être déterminés en même temps aussi précisément que souhaité; cette restriction ne fait pas référence à des insuffisances dans le processus d'observation (par exemple, une mesure inexacte), mais est de nature fondamentale. Ce flou est généralement négligeable dans les systèmes macroscopiques . Cependant, comme leurs effets se développent à volonté dans des systèmes chaotiques, ils prennent tôt ou tard des dimensions macroscopiques (voir effet  papillon ). Avec l'appareil pour dessiner les numéros de loterie avec des boules, c'est le cas après environ 20 coups. La prévisibilité des systèmes chaotiques échoue donc au plus tard à cause de la relation d'incertitude (car elle interdit que les conditions initiales puissent être mesurées avec une quelconque précision). Cela signifie qu'en principe, les systèmes réels ne peuvent pas être déterministes au sens classique , contrairement aux modèles mathématiques qui les décrivent.

Systèmes non linéaires

Un comportement chaotique ne peut se produire que dans des systèmes dont la dynamique est décrite par des équations non linéaires. De telles équations ne sont généralement pas analytiques; H. non pas en spécifiant des quantités explicites, mais uniquement solvables numériquement . La cause de la croissance exponentielle des différences dans les conditions initiales sont souvent des mécanismes d'auto-renforcement, par exemple par rétroaction .

S'il y a une dissipation suffisante due au frottement , un comportement chaotique peut généralement ne pas se développer. Par exemple, dans les manèges forains, qui ont tendance à se comporter de manière chaotique en raison de leur conception, des pics d' accélération inattendus et déraisonnables pourraient se produire sans mesures de freinage appropriées .

L'exemple d'une couche limite montre que les termes dissipatifs n'ont pas seulement un effet stabilisant . Avec la théorie de la stabilité linéaire, on peut montrer que seule l'influence du frottement permet la croissance de petites perturbations. Cette augmentation exponentielle représente la première phase de la transition laminaire-turbulente.

Systèmes discrets

Une foule de Julia

Jusqu'à présent, seul le comportement temporel des systèmes physiques continus a été considéré. Cependant, le chaos est également étudié dans des modèles dans lesquels chaque état passe discrètement dans l' état suivant par une étape d' itération , mathématiquement: des exemples sont l' équation logistique ou la règle d'itération qui conduit aux ensembles de Julia . Les mêmes phénomènes de base peuvent se produire ici que dans les systèmes continus. ${\ displaystyle x_ {n} \ mapsto x_ {n + 1} = f (x_ {n}).}$

En principe, un système discret peut toujours être affecté à un système continu en considérant certains états successifs. Une méthode est la cartographie dite de Poincaré , avec laquelle Henri Poincaré a étudié la stabilité du mouvement planétaire à la fin du 19e siècle .

Phénomènes

Un résultat clé de la recherche sur le chaos est la découverte que les systèmes chaotiques présentent certains modèles de comportement typiques malgré leur comportement apparemment irrégulier qui ne peut être prédit à long terme. Puisqu'ils sont observés dans des systèmes complètement différents, ils sont d'une importance universelle.

Attracteurs étranges

Un phénomène typique dans les processus chaotiques est ce que l'on appelle les attracteurs étranges . Pour le comprendre, on regarde la dynamique du système à l'aide de diagrammes dits d' espace de phase .

Diagrammes d'espace de phase

Les diagrammes d'espace de phase offrent une vue d'ensemble claire de la dynamique d'un système. L'état du système est représenté à tout moment par un point dans un espace dont les axes de coordonnées sont donnés par l'ensemble des variables d'état indépendantes du système et leurs vitesses. La dynamique peut donc être interprétée comme la trajectoire de ce point dans l'espace des phases. Par exemple, l'espace des phases d'un pendule est couvert par l'angle de déviation et la vitesse angulaire associée , et un mouvement de pendule périodique correspond à une courbe fermée autour de l'origine des coordonnées. Mathématiquement, la totalité de tous les comportements possibles peut être interprétée comme un champ de flux dans l'espace des phases.

Attracteurs

Dans certains cas, les systèmes avec des conditions initiales différentes ont tendance à se comporter de la même manière. Les orbites associées dans l'espace des phases convergent alors vers une certaine orbite, appelée attracteur . Dans le cas d'un pendule libre avec frottement, ce serait l'état de repos, c'est-à-dire l'origine des coordonnées dans le diagramme de phase, vers lequel toutes les orbites tendent en spirale. Dans ce cas, il s'agit d'un attracteur en forme de point, un point fixe . Les attracteurs peuvent cependant également être des courbes, comme, par exemple, le cycle limite périodique qui se produit dans un pendule avec frottement qui est excité pour osciller par une force périodique externe . Ce comportement est typique des systèmes dissipatifs . D'un point de vue mathématique, les attracteurs peuvent toujours apparaître lorsque la divergence du champ d'écoulement est négative dans les zones de l'espace des phases. Les points fixes et les cycles limites avec divergence positive sont appelés répulsifs .

L'attracteur étrange

Attracteur de Lorenz dans un espace de phase tridimensionnel basé sur un modèle météorologique simple. Le point de trajectoire tourne dans le sens des aiguilles d'une montre à gauche et dans le sens inverse des aiguilles d'une montre à droite. À chaque révolution, la bande de pistes double et est ensuite coupée en deux moitiés au milieu de l'image pendant le mouvement descendant, de sorte que la décision est prise si la prochaine révolution a lieu à gauche ou à droite. Le caractère chaotique des chemins de fer repose sur ce mécanisme.

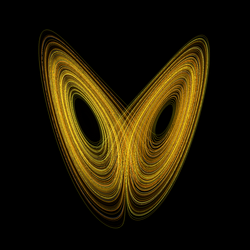
Les systèmes chaotiques peuvent maintenant avoir une forme spéciale d'attracteurs appelés attracteurs étranges. Bien qu'ils soient dans une zone limitée de l'espace des phases, ils sont infiniment longs et non périodiques. En ce qui concerne les petites perturbations, ils présentent un comportement chaotique. Ce sont des fractales avec une structure géométrique interne compliquée et apparemment irrégulière. Ils sont intégrés dans un sous-ensemble de l'espace des phases, qui a une dimensionnalité inférieure à celle de l'espace des phases lui-même, ce qui signifie que dans la dynamique, malgré le caractère chaotique, seule une fraction infinitésimale et donc disparaissante de tous les états possibles se produit. Comme d'habitude avec les fractales, l'attracteur lui-même a une dimension fractale , qui est représentée par un nombre brisé et qui est donc encore plus petite que la dimension de la zone d'enrobage.

L'exemple le plus connu d'un attracteur étrange est l' attracteur de Lorenz , que Lorenz a découvert en modélisant le temps. Un autre exemple est l' attracteur Rössler que Otto E. Rössler est tombé sur quand on regarde une machine de malaxage de bonbons.

Selon le théorème de Poincaré-Bendixson , d'étranges attracteurs ne peuvent apparaître que dans des espaces de phase à partir de trois dimensions. La raison en est que les chemins dans l'espace des phases, comme d'habitude avec un champ d'écoulement, ne se croisent pas, ce qui serait nécessaire pour un comportement chaotique en deux dimensions. Des attracteurs étranges ne peuvent se produire que si au moins un exposant de Lyapunov est négatif et au moins un est positif. Dans un certain sens, le négatif assure la convergence par rapport à une dimension et donc la réduction de la dimensionnalité, le positif pour le comportement chaotique.

Les intersections à travers l'espace des phases, qui sont perpendiculairement percées par des chemins, sont appelées cartographie de Poincaré . Dans le cas d'attracteurs étranges, les points d'intersection forment des ensembles de Cantor .

Des attracteurs étranges tels que l'attracteur de Hénon sont également observés dans des systèmes chaotiques discrets . À l'instar des structures attrayantes, des structures répulsives peuvent également se produire qui sont également fractales, telles que les ensembles de Julia .

Perturbations et résonances

Les systèmes peuvent réagir de manière très sensible aux perturbations et ainsi se transformer rapidement en chaos. Seul le théorème KAM a montré que les influences régulières aux points sensibles de l'espace des phases ne doivent pas nécessairement provoquer un comportement chaotique. Les sensibles sont z. B. relations rationnelles (entières) entre une oscillation non perturbée (par exemple un double pendule) et une excitation périodique. Celles-ci provoquent des résonances (similaires aux résonances orbitales ), c'est pourquoi seules les relations irrationnelles sont considérées pour le théorème.

D'un point de vue mathématique, en particulier dans les imprécisions de mesure qui prévalent normalement, un nombre irrationnel peut être approché par des fractions ( expansion de fraction ). D'où la considération semble pratiquement inutile. Vous devez cependant considérer qu'un système se construira plus rapidement en raison des résonances, plus le rapport de fréquence est proche d'une valeur rationnelle. Cela signifie que les valeurs attendues s'écartent des valeurs mesurées encore plus rapidement que ce ne serait le cas autrement.

Les relations irrationnelles qui ne peuvent être approchées que mal par les ruptures sont donc particulièrement stables vis-à-vis des perturbations (vues en termes de temps). En général, on parle dans ce contexte de nombres nobles , où un rapport appelé nombre d' or est le nombre qui peut être le plus mal approché au moyen de fractions continues et est donc le plus stable face aux influences chaotiques.

La transition vers le chaos

En plus du chaos, les systèmes dynamiques non linéaires peuvent également montrer d'autres comportements, comme la convergence vers un état de repos ou vers un cycle limite périodique. Le comportement qui se produit peut dépendre des conditions initiales ou d'autres paramètres de contrôle . Une représentation graphique des bassins versants correspondants pour certains comportements en fonction de ces paramètres est souvent fractale . La zone de transition vers un comportement chaotique est caractérisée par certaines propriétés, telles que des changements qualitatifs soudains de comportement, également appelés bifurcations .

Période doublant

Diagramme de bifurcation de la séquence de nombres pour l' équation logistique . Les points d'accumulation  x de la séquence sont représentés en fonction du paramètre de contrôle r. A gauche la séquence converge, à droite elle est chaotique, entre elle est périodique. Le doublement de période a lieu aux points de branchement dans la zone de transition.

Lors du passage d'un comportement périodique au chaos, un phénomène connu sous le nom de doublement de période ou scénario du figuier peut se produire . Vers la zone chaotique, la période d'oscillation augmente progressivement d'un facteur deux ( sur le dessin ci-contre). Les intervalles de paramètres associés deviennent de plus en plus courts avec l'augmentation de la période ( ): Le rapport des longueurs d'intervalles de paramètres successifs dans Limes donne à la constante de Feigenbaum un nombre irrationnel . La zone chaotique est fragmentée encore et encore de manière fractale par des intervalles à comportement périodique, qui à leur tour se fondent dans le chaos voisin via un doublement de période. Ce comportement et le rapport numérique associé ne dépendent pas des détails du système non linéaire mathématique ou physique. Ils sont communs à de nombreux systèmes chaotiques. ${\ displaystyle \ Delta r_ {n} \ propto 2 ^ {n},}$ ${\ displaystyle \ Delta x_ {n}}$${\ displaystyle \ Delta x_ {n} \ propto 1/2 ^ {\ delta _ {n}}}$${\ Displaystyle n \ to \ infty}$ ${\ displaystyle \ delta \ approx 4 {,} 669,}$

Intermittence

Outre le doublement des périodes, d'autres formes de transition vers le chaos sont également observées, comme la soi-disant intermittence . Dans le cas d'une valeur de paramètre dans la zone de transition, les comportements quasi-périodiques et chaotiques alternent constamment, la partie chaotique augmentant constamment vers des valeurs de paramètres chaotiques.

Exemples de systèmes chaotiques

Exemples scientifiques

La plupart des processus dans la nature sont basés sur des processus non linéaires. Les systèmes qui peuvent montrer un comportement chaotique sont proportionnellement divers. Voici quelques exemples importants ou bien connus:

• La météo . Pour le moment, la fiabilité des prévisions météorologiques est limitée par la connaissance approximative de l'état initial. Mais même avec des informations complètes, une prévision météorologique à long terme échouerait en fin de compte en raison de la nature chaotique des événements météorologiques . La stabilité du temps peut varier considérablement. Dans certaines conditions météorologiques, les prévisions pour une semaine sont tout à fait possibles, dans d'autres, cependant, à peine pendant 24 heures.
• Le double pendule . Comme il est facile à modéliser et à fabriquer grâce à seulement deux degrés de liberté indépendants, c'est un objet de démonstration populaire pour des changements surprenants dans la séquence chaotique des mouvements. Dans les simulations informatiques et dans les tests, certaines classes de comportement du système peuvent être identifiées, comme le nombre maximum possible de renversements en fonction de l'énergie initiale et du frottement. La machine oscillante Atwood a également deux degrés de liberté, mais un seul corps oscille comme un pendule.
• Le pendule magnétique , dans lequel une boule de fer suspendue à un fil se balance sur plusieurs aimants.
• Systèmes avec balles qui se cognent. Il est important que les sphères se heurtent ou soient réfléchies par des obstacles incurvés afin que les perturbations se développent de manière exponentielle. Des exemples sont le dispositif pour dessiner les numéros de loterie, le flipper et le billard .
• Le problème des trois corps et avec lui notre système solaire ou nos systèmes stellaires constitués de trois étoiles ou plus , comme des amas d'étoiles .
• En médecine , le développement d' embolies mortelles en cas de durcissement des artères, l'échec de certaines fonctions cérébrales lors d'un accident vasculaire cérébral ou le développement de tumeurs malignes après mutations de gènes suppresseurs sont des exemples typiques de comportement chaotique.
• Le rythme cardiaque était parfois considéré comme un signal chaotique. En fonction de l'état de santé, le rythme cardiaque peut être classé à l'aide de critères théoriques du chaos. Cependant, les paramètres calculés dans le processus ne représentent que des valeurs empiriques, les domaines d'application étant la prédiction de la mort subite cardiaque ou, de manière générale, le diagnostic de maladies médiées par le système nerveux autonome. On suppose ici que plus le comportement est chaotique, plus le système est stable. Cependant, considérer le système cardiovasculaire comme «chaotique» est problématique à plusieurs égards.
• Turbulence comme dans l' expérience de Bénard sur la convection .
• La réaction Belousov-Zhabotinsky , une réaction chimique.
• La dynamique des populations dans les modèles prédateurs-proies .
• La transformation du boulanger , un système discret qui regarde l'emplacement d'un raisin sec dans la pâte à gâteau lorsque la pâte est alternativement étalée et pliée.

Exemples issus des sciences humaines et sociales

En plus de ces exemples scientifiques, la recherche sur le chaos est également utilisée dans diverses sciences humaines et sociales pour décrire et expliquer un comportement chaotique. Voici quelques exemples:

• Cours boursiers et développement économique . Mandelbrot avait déjà souligné que de nombreuses courbes de données économiques ont des propriétés non linéaires et peuvent être décrites à l'aide de fractales et d'intermittence.
• Dans les études historiques , la recherche sur le chaos est principalement utilisée pour décrire et expliquer les crises et les états de transition.
• En sciences de la communication , la recherche sur le chaos est utilisée dans le domaine de la recherche sur l' actualité pour mieux expliquer la sélection et la conception des messages.
• En psychologie , la recherche sur le chaos sert d'approche pour expliquer, par exemple, les résultats de la psychologie de la parole sur le bégaiement ou les causes d' actes criminels affectifs (tels que les déchaînements ).

Cependant, dans certains cas, l'utilisation des termes de la théorie du chaos dans les sciences humaines et sociales a été critiquée . L'accusation est que les termes et les résultats de la théorie du chaos sont utilisés pour l'argumentation respective, bien que la définition mathématique / physique d'un système chaotique ne soit pas ou seulement partiellement remplie. Ainsi , la réputation des mathématiques et de la physique est revendiquée sans connexion contextuelle, similaire au processus du nom chute dans la science.

l'histoire

A la fin du XIXe siècle, Henri Poincaré remporte un prix avec une solution à la question de la stabilité du système solaire . Certaines sources affirment qu'il s'agit de l'heure de naissance de la recherche sur le chaos, mais ce n'est qu'au milieu du XXe siècle que la solution de Poincaré a pu être utilement mise en œuvre à l'aide d' ordinateurs .

Les phénomènes chaotiques sont connus depuis longtemps, comme le problème des trois corps ou la turbulence . Pendant longtemps, ces phénomènes ont été considérés comme des cas particuliers plutôt moins courants. Puisqu'une enquête appropriée sans ordinateur semblait peu prometteuse et que presque personne ne s'attendait à des découvertes spéciales, puisque les phénomènes sont entièrement basés sur les concepts de la physique classique, ils ont reçu peu d'attention. Cela n'a changé qu'avec l'avènement d'ordinateurs plus rapides.

Dans les années 1960, Edward N. Lorenz a découvert les phénomènes qui sont maintenant connus sous le nom de chaos déterministe sur un modèle pour le temps avec un ensemble de trois équations pour la mécanique des fluides. Lorsqu'il a utilisé des valeurs arrondies d'un calcul antérieur pour gagner du temps, il a observé que de minuscules changements dans les conditions initiales conduisaient à des résultats complètement différents après un court laps de temps. L'effet papillon qui en découle et la formulation du concept de dépendance sensible aux conditions initiales sont souvent devenus des métaphores mal interprétées de la «théorie du chaos».

En 1976, Robert May a simulé une population de poissons avec un taux de croissance en utilisant la formule pour représenter des ressources limitées avec le terme . Il a choisi une très petite population initiale de 2% pour sa simulation informatique et a découvert que son modèle de calcul s'installe avec un taux de croissance autour d' un comportement chaotique.${\ displaystyle P}$${\ displaystyle R}$${\ displaystyle P _ {\ text {nouveau}} = R \ cdot P _ {\ text {ancien}} \ cdot (1-P _ {\ text {ancien}}),}$${\ displaystyle 1-P _ {\ text {alt}}}$${\ displaystyle R}$${\ displaystyle 3 {,} 8}$

Dans les années 1970 à 1980, Mitchell Feigenbaum a découvert les phénomènes de l' équation logistique et de la constante de Feigenbaum qui porte son nom . Cette équation correspond à l' ensemble de Mandelbrot étudié par Benoit Mandelbrot en 1980 , puisqu'elle est également basée sur une équation quadratique.

À peu près à la même époque, Siegfried Großmann à Marburg et Hermann Haken à Stuttgart travaillaient à la formulation de leurs théories, qui furent bientôt inspirées par les idées sur Mandelbrot et Feigenbaum. Großmann a formulé une description du laser à l'aide de la dynamique non linéaire, et Haken est considéré comme le fondateur de la synergie et le découvreur du soi-disant principe d' asservissement . L'ensemble de Mandelbrot, populairement connu sous le nom d '«homme-pomme», est considéré comme l'une des fractales les plus riches en formes connues.

À partir des années 1980, des groupes de travail ont été créés dans de nombreuses universités, telles que B. à Graz, Vienne ou Ratisbonne. A Munich, le «Chaos Group de l'Université technique de Munich», dirigé par Alfred Hübler , a mené de nombreux projets de recherche à la Chaire de physique E13 ( Edgar Lüscher ). Après la mort de Lüscher, il s'est organisé en association de recherche et a organisé une série de séries de conférences et plusieurs conférences annuelles, au cours desquelles on a tenté de représenter tout le spectre de la recherche sur le chaos et de permettre un dialogue interdisciplinaire. Grands instituts de recherche tels que B. le Santa Fe Institute (USA) ou l'Institute for Nonlinear Dynamics de Potsdam.

La recherche actuelle s'intéresse davantage à un ensemble incohérent de phénomènes et de théories. De nombreux chercheurs qui traitent encore du sujet aujourd'hui ne se décriraient plus comme des chercheurs du chaos.

Littérature

• Herrmann, Dietmar: Algorithms for Chaos and Fractals 1ère édition, Addison-Wesley, Bonn et autres. 1994.
• Paul Davies: Principe du chaos. Le nouvel ordre du cosmos. ("Plan cosmique"). Goldmann, Munich 1991, ISBN 3-442-11469-1 .
• Bruno Eckhardt: Chaos. Fischer, Francfort-sur-le-Main 2004, ISBN 3-596-15569-X .
• James Gleick : Chaos, l'ordre de l'univers. Repousser les limites de la physique moderne. ("Chaos. Faire une nouvelle science"). Droemer Knaur, Munich 1990, ISBN 3-426-04078-6 .
• Günter Küppers (Ed.): Chaos et ordre. Formes d'auto-organisation dans la nature et la société. Reclam, Ditzingen 1996, ISBN 3-15-009434-8 .
• Wolfgang Metzler: Dynamique non linéaire et chaos , BG Teubner, Stuttgart, Leipzig 1998, ISBN 3-519-02391-1
• Gregor Morfill , Herbert Scheingraber: Le chaos est partout ... et ça marche. Une nouvelle vision du monde. Ullstein, Francfort-sur-le-Main 1993, ISBN 3-548-35343-6 .
• Peter Smith: Expliquer le chaos. Cambridge University Press, Cambridge 1994. Travail standard sur la philosophie de la théorie du chaos.
• Marco Wehr: Le défaut du papillon. Turbulence dans la théorie du chaos. Klett-Cotta, Stuttgart 2002, ISBN 3-608-94322-6 .
• Karin S. Wozonig: Théorie du chaos et études littéraires. Studienverlag, Innsbruck, Vienne 2008, ISBN 978-3-7065-4507-5 , version en ligne (PDF) .
• Heinz Georg Schuster : Chaos déterministe. VCH, Weinheim 1994, ISBN 3-527-29089-3 .
• Otto E. Rössler , Jürgen Parisi, Joachim Peinke et Ruedi Stoop: rencontre avec le chaos. Complexité hiérarchique auto-organisée dans les expériences de semi-conducteurs. Springer, Berlin 1992, ISBN 3-540-55647-8 .

liens web

Wiktionnaire: théorie du chaos  - explications des significations, origines des mots, synonymes, traductions

• Robert Bishop:  Chaos. Dans: Edward N. Zalta (Ed.): Stanford Encyclopedia of Philosophy .
• Introduction à la recherche sur le chaos. Ancienne conférence à l'Université des sciences appliquées de Munich.
• C. Wolfseher: Un (-) regard sur le chaos - systèmes dynamiques non linéaires.
• Frank Grotelüschen: Apple man en marge. Qu'est-il arrivé à la théorie du chaos? DRadio, 13 novembre 2005. Avec quatre exemples d'application actuels.
• Test interactif de processus chaotiques. Site Web de Robert Doerner

Preuve individuelle

1. ↑ Ralph Abraham, Yoshisuke Ueda: L'Avant-garde du Chaos: Souvenirs des premiers jours de la théorie du chaos . World Scientific, 2000, ISBN 978-981-02-4404-0 . P. 91.
2. ↑ Tito Arecchi , Riccardo Meucci: Chaos in lasers, Scholarpedia 2008
3. ↑ avec${\ displaystyle f (t, U) = \ {f (t, u) \ mid u \ in U \}}$
4. ↑ Charlotte Werndl: Quelles sont les nouvelles implications du chaos pour l'imprévisibilité? (2009). Dans: The British Journal for the Philosophy of Science. 60, 195-220.
5. ↑ Albert Christmann: Applications de la synergie et de la théorie du chaos dans l'économie. Karlsruhe 1990.
6. ↑ Otto Loistl, Iro Betz: Chaostheorie. Sur la théorie des systèmes dynamiques non linéaires. Munich 1993.
7. ↑ Bernd-Olaf Küppers : Chaos et histoire. Les événements mondiaux peuvent-ils être exprimés dans des formules? In: Reinhard Breuer (Hrsg.): Le battement des ailes du papillon. Une nouvelle vision du monde grâce à la recherche sur le chaos. Herne 1993.
8. ^ Walter L. Bühl : Changement social dans le déséquilibre. Cycles, fluctuations, catastrophes. Stuttgart 1990.
9. ^ Stefan Frerichs: Le journalisme comme chaos constructif. Dans: Martin Löffelholz , Liane Rothenberger (Hrsg.): Handbuch Journalismustheorien. Wiesbaden 2016, p. 191 et suiv.
10. ↑ Rainer Höger: Recherche sur le chaos et ses perspectives pour la psychologie. Dans: Psychological Rundschau. 43e vol., N ° 4, Göttingen 1992, p. 223 et suiv.
11. ↑ Thomas Fabian , Michael Stadler : Une approche théorique du chaos du comportement délinquant dans les situations de stress psychosocial. Dans: Gestalt Theory, Une revue multidisciplinaire internationale. 13e année, numéro 2/1991, Opladen 1991, p. 98 et suiv.
12. ^ Robert M. May: Modèles mathématiques simples avec une dynamique très compliquée. Nature 261 (1976) 459-467.

Cette version a été ajoutée à la liste des articles à lire le 14 janvier 2006 .