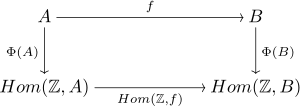groupe abélien

Un groupe abélien est un groupe pour lequel la loi commutative s'applique également .

Le terme mathématique groupe abélien , également appelé groupe commutatif , généralise l'arithmétique avec les nombres. L'addition de nombres rationnels et la multiplication de nombres rationnels satisfont à un certain nombre de lois communes. Ces règles se retrouvent souvent en géométrie et en algèbre. Par exemple, avec déplacements, rotations du plan autour d'un point, addition de fonctions. Les ornements dans l'art et la nature retracent les traces des groupes abéliens. Par conséquent, la signification particulière du signe d' addition et du signe de multiplication est abstraite et le concept du groupe commutatif ou abélien est créé. Le nom a été choisi en l' honneur du mathématicien norvégien Niels Henrik Abel . ${\ style d'affichage \ neq 0}$${\ style d'affichage +}$${\ style d'affichage \ cdot}$

définition

Soyez un lot . Exactement un élément est affecté à chaque paire . Le couple est appelé groupe abélien si la connexion satisfait aux lois suivantes : ${\ style d'affichage G}$${\ displaystyle (a, b) \ in G \ times G}$${\ displaystyle a * b \ in G}$${\ style d'affichage (G, *)}$${\ displaystyle * \ deux-points \, G \ times G \ to G, (a, b) \ mapsto a * b}$

1. Droit associatif : Pour tous s'appliquent : .${\ displaystyle a, b, c \ in G}$${\ displaystyle a * (b * c) = (a * b) * c}$
2. Commutatif : Pour tout ce qui suit s'applique : .${\ displaystyle a, b \ in G}$${\ style d'affichage a * b = b * a}$
3. Élément neutre : Il existe un élément , tel que pour tout ce qui suit s'applique : .${\ displaystyle e \ dans G}$${\ displaystyle a \ in G}$${\ displaystyle a * e = a}$
4. Élément inverse : pour chacun il y a un avec .${\ displaystyle a \ in G}$${\ displaystyle a ^ {- 1} \ in G}$${\ displaystyle a * a ^ {- 1} = e}$

Un groupe est dit non abélien s'il existe au moins une paire avec . ${\ style d'affichage (G, *)}$${\ style d'affichage (a, b)}$${\ displaystyle a * b \ neq b * a}$

Explications

• Si la loi commutative est omise des axiomes, un groupe résulte . Un groupe abélien n'est donc rien de plus qu'un groupe pour lequel la loi commutative s'applique également.
• L'élément neutre et l'élément inverse de chaque élément du groupe sont clairement définis, comme le montrent les axiomes.
• Habituellement, un groupe abélien est écrit de manière additive avec le symbole du lien et ensuite appelé module . Dans ce cas la somme de et , l'élément neutre est appelé élément zéro ou simplement zéro et s'écrit. L'inverse de est alors noté comme son opposé avec .${\ style d'affichage +}$${\ style d'affichage a + b}$${\ style d'affichage a}$${\ style d'affichage b}$${\ style d'affichage 0}$${\ style d'affichage a}$${\ style d'affichage -a}$
• Un groupe commutatif peut également être écrit de manière multiplicative avec le symbole du lien . Alors ou est simplement le produit de et . Dans ce cas, l'élément neutre s'appelle un élément ou simplement un et s'écrit. L'inverse de s'appelle maintenant .${\ style d'affichage \ cdot}$${\ displaystyle a \ cdot b}$${\ style d'affichage de}$${\ style d'affichage a}$${\ style d'affichage b}$${\ style d'affichage 1}$${\ style d'affichage a}$${\ displaystyle a ^ {- 1}}$
• Dans un module, la différence entre deux éléments est expliquée par . Les règles s'appliquent alors : . Si le groupe abélien s'écrit multiplicativement, le quotient est défini en conséquence .${\ displaystyle from: = a + (- b)}$${\ displaystyle - (a + b) = (- a) + (- b), - (ab) = (- a) + b}$${\ displaystyle a / b: = a \ cdot b ^ {- 1}}$

Exemples

1. ${\ style d'affichage (\ mathbb {Z}, +)}$est le principal groupe abélien. Où est l'ensemble des nombres entiers et l'addition habituelle.${\ displaystyle \ mathbb {Z}}$${\ style d'affichage +}$
2. ${\ displaystyle (\ mathbb {Q} ^ {*}, \ cdot)}$est un groupe abélien. C'est l'ensemble des nombres rationnels sans et c'est la multiplication ordinaire.${\ displaystyle \ mathbb {Q} ^ {*}}$${\ style d'affichage 0}$${\ style d'affichage \ cdot}$
3. L'ensemble des nombres décimaux finis n'est pas un groupe abélien en termes de multiplication. Par exemple, le nombre n'a pas d'inverse par rapport à la multiplication. ne peut pas être écrit comme une fraction décimale finie. En ce qui concerne l'addition normale, les fractions décimales finies forment un groupe abélien.${\ style d'affichage 3}$${\ displaystyle {\ frac {1} {3}}}$
4. L'ensemble des déplacements dans le plan euclidien forme un groupe abélien. Le lien est l'exécution séquentielle des quarts de travail.
   

   Un triangle autour du vecteur de déplacement reporté${\ displaystyle {\ vec {v}}}$
5. L'ensemble des rotations dans un plan autour d'un point forme un groupe abélien. Le lien est l'exécution séquentielle des rotations.
6. L'ensemble des torsions s'étend dans un plan forme un groupe abélien.
7. Le tableau de liaison peut être rédigé par des groupes suffisamment petits. S'il s'agit du tableau d'un groupe abélien, le tableau est symétrique à la diagonale principale . Ce tableau se pose, par exemple, si l'on considère les rotations d'un triangle équilatéral autour du centre de gravité, qui transforment le triangle en lui-même. est le demi-tour , est le demi-tour et est le demi-tour .${\ displaystyle {\ begin {matrice} * | & e | & a | & b | \\\ hline \ hline e | & e | & a | & b | \\\ hline a | & a | & b | & e | \\\ hline b | & b | & e | & a | \\\ hline \ end {matrice}}}$${\ style d'affichage e}$${\ displaystyle 0 ^ {\ circ}}$${\ style d'affichage a}$${\ displaystyle 120 ^ {\ circ}}$${\ style d'affichage b}$${\ displaystyle 240 ^ {\ circ}}$
8. S'il y a des groupes abéliens, alors à travers devient un groupe abélien .${\ style d'affichage A, B}$${\ displaystyle A \ times B = \ {(a, b) | a \ in A, \ b \ in B \}}$${\ displaystyle (a, b) + (a ', b'): = (a + a ', b + b')}$
9. Est un ensemble et un groupe abélien, c'est un groupe quand il est défini . C'est ce qu'on appelle le e composant de . Souvent, la forme est écrite sous forme de vecteur . C'est . Est , alors est l'ensemble des séquences, où les termes de la séquence sont des éléments de . Est ainsi .${\ style d'affichage I}$${\ style d'affichage A}$${\ displaystyle A ^ {I}: = \ {f | f \ deux-points I \ to A \}}$${\ displaystyle (f + g) (i): = f (i) + g (i)}$${\ style d'affichage f (i)}$${\ style d'affichage i}$${\ style d'affichage f}$${\ style d'affichage f}$${\ style d'affichage (a_ {i})}$${\ displaystyle a_ {i} = f (i)}$${\ displaystyle I = \ mathbb {N}}$${\ displaystyle A ^ {\ mathbb {N}}}$${\ style d'affichage A}$${\ displaystyle I = \ {1, \ points, n \}}$${\ displaystyle \ mathbb {Z} ^ {n} = \ {(a_ {1}, \ points, a_ {n}) | {\ text {with}} a_ {i} \ in \ mathbb {Z} \} }$
10. Les nombres réels forment un groupe abélien avec l'addition ; sans le zéro ils forment un groupe abélien avec la multiplication.
11. Plus généralement, chaque corps donne deux groupes abéliens et de la même manière .${\ style d'affichage (K, +, \ cdot)}$${\ displaystyle \ left (K, + \ right)}$${\ displaystyle (K \ setminus \ {0 \}, \ cdot)}$
12. En revanche, le groupe des matrices inversibles sur un corps pour un exemple de groupe non abélien. Soit dit en passant, le plus petit groupe non abélien est le groupe symétrique S ₃ à six éléments.${\ displaystyle (\ mathrm {GL} _ {n} (K), \ cdot)}$${\ style d'affichage (n \ fois n)}$ ${\ style d'affichage K}$${\ style d'affichage n> 1}$

Sous-groupes

Un sous-ensemble non vide du groupe abélien est appelé sous - groupe s'il est lui-même un groupe au regard de l'opération de groupe. C'est exactement le cas lorsque tout ce qui suit s'applique : . Dans cet article, la notation suivante est sélectionnée : . ${\ style d'affichage U}$${\ style d'affichage A}$${\ displaystyle a, b \ in U}$${\ displaystyle de \ dans U}$${\ displaystyle U \ hookrightarrow A}$

1. ${\ displaystyle \ mathbb {Z}}$est un sous-groupe de .${\ displaystyle \ mathbb {Q}}$
2. La moyenne des sous-groupes est un sous-groupe.
3. Est un groupe et , alors et sont des sous - groupes de . Par exemple, un ensemble de nombres pairs est un sous-ensemble de .${\ style d'affichage A}$${\ displaystyle n \ in \ mathbb {N}}$${\ displaystyle A [n]: = \ {a | a \ in A, a \ cdot n = 0 \}}$${\ displaystyle A \ cdot n: = \ {a \ cdot n | a \ in A \}}$${\ style d'affichage A}$${\ displaystyle 2 \ cdot \ mathbb {Z} = \ {a \ cdot 2 | a \ in \ mathbb {Z} \} = \ mathbb {Z} \ cdot 2 =}$${\ displaystyle \ mathbb {Z}}$
4. Chaque sous - ensemble est contenu dans un plus petit sous-groupe, qui contient. Ce sous-groupe est appelé le sous - groupe de créé par . Il est désigné par.${\ displaystyle U \ sous-ensemble A}$${\ style d'affichage U}$${\ style d'affichage U}$ ${\ style d'affichage A}$${\ displaystyle \ left \ langle U \ right \ rangle}$
5. S'il y a des sous - groupes de , alors l'ensemble est un sous-groupe de . Plus général : si une famille est de sous-groupes, alors est un sous-groupe de . On l'appelle la somme des sous-groupes .${\ style d'affichage U, V}$${\ style d'affichage A}$${\ displaystyle U + V: = \ {u + v \ vert u \ in U, v \ in V \}}$${\ style d'affichage A}$${\ displaystyle (U_ {i} | i \ in I)}$${\ displaystyle \ sum \limits _ {i \ in I} U_ {i}: = \ {\ sum _ {i \ in I} u_ {i} \ vert u_ {i} \ in U_ {i} \}}$${\ style d'affichage A}$
6. Est , alors est le sous - groupe créé par . Est-ce que c'est le nom d' un système générateur de .${\ displaystyle U \ sous-ensemble A}$${\ style d'affichage U}$${\ displaystyle \ left \ langle U \ right \ rangle = \ sum _ {u \ in U} \ left \ langle u \ right \ rangle}$${\ displaystyle \ left \ langle U \ right \ rang = A}$${\ style d'affichage U}$${\ style d'affichage A}$
7. Un groupe abélien est dit de type fini s'il existe un sous-ensemble fini tel que . S'il est généré par un élément , il est dit cyclique . C'est écrit.${\ style d'affichage A}$${\ displaystyle U \ sous-ensemble A}$${\ displaystyle \ left \ langle U \ right \ rang = A}$${\ style d'affichage A}$${\ displaystyle a \ dans A}$${\ style d'affichage A}$ ${\ displaystyle A = a \ cdot \ mathbb {Z}}$
   1. Chaque sous-groupe de est cyclique.${\ displaystyle \ mathbb {Z}}$
   2. Cela signifie, par exemple : La somme de deux sous-groupes cycliques de est à nouveau cyclique. Il s'applique . Où est le
   plus grand facteur commun de . Par exemple : .${\ displaystyle \ mathbb {Z}}$${\ displaystyle a \ cdot \ mathbb {Z} + b \ cdot \ mathbb {Z} = \ operatorname {ggT} (a, b) \ cdot \ mathbb {Z}}$${\ displaystyle \ operatorname {ggT} (a, b)}$${\ style d'affichage a, b}$${\ displaystyle 6 \ cdot \ mathbb {Z} +9 \ cdot \ mathbb {Z} = 3 \ cdot \ mathbb {Z}}$
8. Sont des sous - ensembles de , alors est . Où est le plus petit multiple commun de . Par exemple .${\ displaystyle a \ cdot \ mathbb {Z}, b \ cdot \ mathbb {Z}}$${\ displaystyle \ mathbb {Z}}$${\ displaystyle a \ cdot \ mathbb {Z} \ cap b \ cdot \ mathbb {Z} = \ operatorname {kgV} (a, b) \ cdot \ mathbb {Z}}$${\ displaystyle \ operatorname {kgV} (a, b)}$${\ style d'affichage a, b}$${\ displaystyle 3 \ mathbb {Z} \ cap 5 \ mathbb {Z} = 15 \ mathbb {Z}}$
9. ${\ style d'affichage (\ mathbb {Q}, +)}$n'est pas de génération finie. Plus précisément : si un système générateur est et est , alors il y a aussi un système générateur.${\ style d'affichage U}$${\ style d'affichage (\ mathbb {Q}, +)}$${\ displaystyle u \ in U}$${\ displaystyle U \ setminus \ {u \}}$

• Quelques groupes en art et nature
• 

  Fra Giovanni da Verona a peint ce tableau comme incrustation dans la Sacrestia de Santa Maria in Organo. Il illustre un groupe cyclique d'ordre 8 comprenant un sous-groupe d'ordre 4.

• 

  Conception de Bramante pour la basilique Saint-Pierre. Il s'agit entre autres d'un groupe tournant d'ordre 4. En fait, mathématiquement encore plus s'y cache. C'est une fractale.

• 

  La fleur montre la symétrie du groupe en rotation d'ordre 5. Le pentagramme est également clairement visible.

Groupes de facteurs

S'il s'agit d' un sous-groupe, alors définit une relation d'équivalence. Sont et sont ainsi . La relation d'équivalence est dite compatible avec l'addition. Soit l' ensemble des classes d'équivalence. Sur est expliqué un ajout. ${\ displaystyle U \ hookrightarrow A}$${\ displaystyle a \ sim a '\ iff a-a' \ in U}$${\ displaystyle a, a ', b, b' \ in A}$${\ displaystyle a \ sim a ', b \ sim b'}$${\ displaystyle a + b \ sim a '+ b'}$${\ displaystyle A / U: = \ {a + U | a \ in A \} =}$${\ style d'affichage A / U}$

${\ displaystyle (a + U) + (b + U) \ deux-points = (a + b) + U}$.

Si l'on veut vraiment calculer en, il suffit de se limiter à un système de représentants de . Parce que chaque classe d'équivalence est déterminée de manière unique par un élément de la classe d'équivalence. C'est . ${\ style d'affichage A / U}$${\ style d'affichage A / U}$${\ displaystyle a \ sim a '\ iff a + U = a' + U}$

• Est un sous-groupe de , alors est cyclique. C'est-à-dire qu'il y en a un avec . S'il y a un représentant positif dans la classe d'équivalence de . Ce n'est donc pas une limitation si l'on présuppose. On obtient un représentant de en divisant avec le reste.Il est positif pour deux si et seulement s'ils laissent le même reste en divisant . C'est alors un système de représentants de . Désigne le radical lors du partage par résultats, donc le calcul correspond à : l'« addition » suivante pour . L'index du signe est omis. Ainsi dans, par exemple .${\ displaystyle U \ hookrightarrow \ mathbb {Z}}$${\ displaystyle \ mathbb {Z}}$${\ style d'affichage U}$${\ displaystyle n \ in \ mathbb {N}}$${\ displaystyle U = n \ cdot \ mathbb {Z}}$${\ displaystyle a \ in U}$${\ style d'affichage a}$${\ displaystyle a \ in \ mathbb {N}}$${\ style d'affichage a + U}$${\ displaystyle a \ sim a '}$${\ style d'affichage n}$${\ displaystyle \ {0, \ points, n-1 \}}$${\ displaystyle \ mathbb {Z} / n \ cdot \ mathbb {Z}}$${\ displaystyle a \ mod n}$${\ style d'affichage a}$${\ style d'affichage n}$${\ displaystyle \ mathbb {Z} / n \ cdot \ mathbb {Z}}$${\ displaystyle a + _ {n} b: = (a + b) \ mod n}$${\ displaystyle a, b \ in \ {0, \ points, n-1 \}}$${\ style d'affichage n}$${\ style d'affichage +}$${\ displaystyle \ mathbb {Z} / 11 \ cdot \ mathbb {Z}}$${\ displaystyle 7 + 5 = 1 {\ bmod {1}} 1}$
• ${\ displaystyle \ mathbb {Z}}$est un sous-groupe de . Un système de représentants de est l'intervalle unitaire ouvert à droite . Dans ce Repräsentantesystem est attendu comme suit : . Où est le plus grand entier . C'est donc pour :${\ displaystyle \ mathbb {R}}$${\ displaystyle \ mathbb {R} / \ mathbb {Z}}$${\ style d'affichage [0.1 [}$${\ displaystyle (a + b) {\ bmod {1}} = (a + b) - [a + b]}$${\ style d'affichage [x] : =}$${\ style d'affichage \ leq x}$${\ displaystyle a, b \ dans [0,1 [}$${\ displaystyle (a + b) {\ bmod {1}} = {\ begin {cases} a + b {\ text {fall}} a + b <1 \\ a + b-1 {\ text {if} } a + b \ geq 1 \ end {cas}}}$
• Les propriétés spéciales du sous-groupe de sont discutées un peu plus loin.${\ displaystyle \ mathbb {Q} / \ mathbb {Z}}$${\ displaystyle \ mathbb {R} / \ mathbb {Z}}$

Homomorphismes

définition

Sont des groupes abéliens, est une illustration de l' homomorphisme si pour tout s'applique : .${\ style d'affichage A, B}$${\ displaystyle f \ deux points A \ rightarrow B}$ ${\ displaystyle a, b \ in A}$${\ displaystyle f (a + b) = f (a) + f (b)}$

Exemples d'homomorphismes

• L'identité et l'application nulle sont toujours des homomorphismes. Il existe exactement un morphisme pour chaque groupe abélien . Il existe exactement un homomorphisme de la même manière .${\ displaystyle A \ ni a \ mapsto 0 \ in B}$${\ style d'affichage A}$${\ style d'affichage 0 \ à A}$${\ displaystyle A \ à 0}$
• Si un sous-groupe de , la carte d'inclusion est un homomorphisme.${\ displaystyle U \ hookrightarrow A}$${\ style d'affichage A}$
• L'application est un homomorphisme. Général : Si c'est le cas , la multiplication avec , c'est-à-dire l'application , est un homomorphisme. C'est l'équivalent de distributive , qui dit : Pour tout ce qui suit s'applique : . Les multiplications sont aussi les seuls homomorphismes qui signifient : S'il y a un homomorphisme, il y en a un avec pour tout .${\ displaystyle 2 * \ colon \ mathbb {Z} \ ni x \ mapsto 2 \ cdot x \ in \ mathbb {Z}}$${\ displaystyle a \ in \ mathbb {Z}}$${\ style d'affichage a}$${\ displaystyle a * \ colon \ mathbb {Z} \ ni x \ mapsto a \ cdot x \ in \ mathbb {Z}}$${\ displaystyle a, b, c \ in \ mathbb {Z}}$${\ displaystyle a \ cdot (b + c) = a \ cdot b + a \ cdot c}$${\ displaystyle \ mathbb {Z} \ à \ mathbb {Z}}$${\ displaystyle f \ deux-points \ mathbb {Z} \ à \ mathbb {Z}}$${\ displaystyle a \ in \ mathbb {Z}}$${\ displaystyle f (z) = a \ cdot z}$${\ displaystyle z \ in \ mathbb {Z}}$
• Si , l'application est un homomorphisme, du groupe additif au groupe multiplicatif .${\ displaystyle a \ in \ mathbb {Q} ^ {*}}$${\ displaystyle \ mathbb {Z} \ ni x \ mapsto a ^ {x} \ in \ mathbb {Q}}$${\ displaystyle \ mathbb {Z}}$${\ displaystyle \ mathbb {Q} ^ {*}}$
• La fonction exponentielle naturelle : est un homomorphisme de groupes abéliens. Il mappe bijectivement le groupe additif dans le groupe multiplicatif . L'application inverse est le logarithme népérien .${\ displaystyle \ exp \ colon \ mathbb {R} \ ni x \ mapsto \ exp (x) = e ^ {x} \ in \ mathbb {R} ^ {+}}$${\ displaystyle \ mathbb {R}}$${\ displaystyle \ mathbb {R} ^ {+}}$
• La concaténation d'homomorphismes est un homomorphisme. La classe des groupes abéliens, avec les homomorphismes, forment une catégorie (mathématiques) . C'est le prototype d'une catégorie abélienne .${\ displaystyle {\ mathcal {A}}}$

Propriété universelle des nombres entiers

• Chaque groupe et chaque il y a exactement un homomorphisme avec . C'est alors , et . Le général est${\ style d'affichage A}$${\ displaystyle a \ dans A}$${\ displaystyle \ Phi _ {a} \ deux-points \, \ mathbb {Z} \ à A}$${\ displaystyle \ Phi _ {a} (1) = a}$${\ displaystyle \ Phi _ {a} (2) = a * a}$${\ displaystyle \ Phi _ {a} (- 1) = a ^ {- 1}}$

${\ displaystyle \ Phi _ {a} (z) = \ left \ {{\ begin {matrix} \ underbrace {a + a + \ ldots + a} _ {z \ \ mathrm {times}} & {\ text { if }} & z \ geq 0, \\ - (\ Phi _ {a} (| z |)) & {\ text {if}} & z <0. \\\ end {matrice}} \ right.}$.

C'est un groupe abélien libre avec une base . ${\ style d'affichage (\ mathbb {Z}, +)}$${\ style d'affichage \ {1 \}}$

• Elle est proche de et pour définir : . Ce qui suit s'applique alors :${\ displaystyle z \ in \ mathbb {Z}}$${\ displaystyle a \ dans A}$${\ displaystyle a \ cdot z: = \ Phi _ {a} (z)}$

1. ${\ displaystyle a \ cdot 0 = 0}$. (Attention ! Il peut être déroutant que le même signe soit utilisé des deux côtés de l'équation . Sur le côté gauche de l'équation se trouve l'élément neutre dans . Sur le côté droit de l'équation se trouve l'élément neutre dans . Les deux fois sont le différents éléments neutres avec écrit.)${\ style d'affichage 0}$${\ displaystyle \ mathbb {Z}}$${\ style d'affichage A}$${\ style d'affichage 0}$
2. Car tout le monde est .${\ displaystyle a \ dans A}$${\ displaystyle a \ cdot 1 = a}$
3. Car tout et tout est .${\ displaystyle z_ {1}, z_ {2} \ in \ mathbb {Z}}$${\ displaystyle a \ dans A}$${\ displaystyle a \ cdot (z_ {1} \ cdot z_ {2}) = (a \ cdot z_ {1}) \ cdot z_ {2}}$
4. Car tout et tout est .${\ displaystyle a \ dans A}$${\ displaystyle z_ {1}, z_ {2} \ in \ mathbb {Z}}$${\ displaystyle a \ cdot (z_ {1} + z_ {2}) = a \ cdot z_ {1} + a \ cdot z_ {2}}$
5. Car tout et tout est .${\ displaystyle a_ {1}, a_ {2} \ dans A}$${\ displaystyle z \ in \ mathbb {Z}}$${\ displaystyle (a_ {1} + a_ {2}) \ cdot z = a_ {1} \ cdot z + a_ {2} \ cdot z}$

• De cette façon, chaque module devient un module . Est un homomorphisme, alors pour tout : .${\ displaystyle \ mathbb {Z}}$${\ displaystyle f \ deux-points \, A \ à B}$${\ displaystyle a \ in A, z \ in Z}$${\ displaystyle f (a \ cdot z) = f (a) \ cdot z}$

• Il vaut la peine de traduire l'avant-dernière déclaration d'un groupe qui est écrite de manière multiplicative. Dans ce cas, l'élément neutre est dans le . Pour chaque arbitraire, il y a exactement un homomorphisme avec . C'est . Le général est . Les lois ci-dessus disent alors :${\ style d'affichage (Q, \ cdot)}$${\ style d'affichage Q}$${\ style d'affichage 1}$${\ displaystyle q \ dans Q}$${\ displaystyle \ Phi _ {q} \ deux-points \, \ mathbb {Z} \ à Q}$${\ displaystyle \ Phi _ {q} (1) = q}$${\ displaystyle \ Phi _ {q} (2) = q \ cdot q = q ^ {2}, \ Phi _ {q} (- 1) = q ^ {- 1}}$${\ displaystyle \ Phi _ {q} (z) = q ^ {z}}$

1. Car tout le monde est .${\ displaystyle q \ dans Q}$${\ displaystyle q ^ {0} = 1}$
2. Car tout le monde est .${\ displaystyle q \ in Q, z_ {1}, z_ {2} \ in Z}$${\ displaystyle q ^ {(z_ {1} \ cdot z_ {2})} = (q ^ {z_ {1}}) ^ {z_ {2}}}$
3. Car tout le monde est .${\ displaystyle q \ in Q, z_ {1}, z_ {2} \ in Z}$${\ displaystyle q ^ {z_ {1} + z_ {2}} = q ^ {z_ {1}} \ cdot q ^ {z_ {2}}}$
4. Car tout le monde est . Si des nombres rationnels ou réels sont substitués à l'ensemble , alors les lois connues de l'école pour le calcul avec les exposants en résultent.${\ displaystyle q_ {1}, q_ {2} \ dans Q, z \ dans Z}$${\ displaystyle (q_ {1} \ cdot q_ {2}) ^ {z} = q_ {1} ^ {z} \ cdot q_ {2} ^ {z}}$${\ style d'affichage Q}$${\ style d'affichage \ neq 0}$

Propriétés des homomorphismes

Est un homomorphisme, et sont respectivement des sous-groupes, puis et sont des sous - groupes. En particulier, et sont des sous - groupes. Il en découle : ${\ displaystyle \ alpha \ deux-points A \ à B}$${\ displaystyle U \ hookrightarrow A}$${\ displaystyle V \ hookrightarrow B}$${\ displaystyle \ alpha ^ {- 1} (V) \ hookrightarrow A}$${\ displaystyle \ alpha (U) \ hookrightarrow B}$${\ displaystyle \ operatorname {core} (\ alpha): = \ {a | a \ in A, \ alpha (a) = 0 \}}$${\ displaystyle \ alpha (A): = \ operatorname {image} (\ alpha) = \ {\ alpha (a) | a \ in A \}}$

• Est un groupe et un nombre naturel, alors et sont des sous - groupes de . C'est vrai parce que la multiplication par est un homomorphisme.${\ style d'affichage A}$${\ style d'affichage n}$${\ displaystyle A \ cdot n: = \ {a \ cdot n | a \ in A \}}$${\ displaystyle A [n]: = \ {a | a \ cdot n = 0 \}}$${\ style d'affichage A}$${\ style d'affichage n}$
• ${\ displaystyle T (A) : = \ sum \limits _ {n \ in \ mathbb {N}} A [n] = \ {a | a \ in A {\ text {il y a}} n \ in \ mathbb {N} {\ text {with}} a \ cdot n = 0 \}}$est un sous-groupe de . C'est le sous - groupe de torsion de . Est , il est appelé sans torsion . Pour chaque groupe est sans torsion. Le sous-groupe de torsion de est .${\ style d'affichage A}$${\ style d'affichage A}$${\ style d'affichage T (A) = 0}$${\ style d'affichage A}$ ${\ style d'affichage A / T (A)}$${\ displaystyle \ mathbb {R} / \ mathbb {Z}}$${\ displaystyle \ mathbb {Q} / \ mathbb {Z}}$
• Si un homomorphisme est produit par des éléments et est produit par des éléments, alors est produit par des éléments.${\ displaystyle f \ deux-points A \ à B}$${\ displaystyle \ operatorname {core} (f)}$${\ style d'affichage n}$${\ displaystyle \ operatorname {image} (f)}$${\ style d'affichage m}$${\ style d'affichage A}$${\ style d'affichage n + m}$
• Chaque sous-groupe de est généré à partir d'un maximum d' éléments.${\ displaystyle \ mathbb {Z} ^ {n}}$${\ style d'affichage n}$

Homomorphismes injectifs

• S'il existe un homomorphisme bijectif, l'application inverse est également un homomorphisme. Dans ce cas, on parle d' isomorphisme . Existe-t-il un isomorphisme entre et soi-disant isomorphe .${\ displaystyle \ alpha \ deux-points A \ à B}$${\ displaystyle \ alpha ^ {- 1} \ deux points B \ à A}$${\ style d'affichage \ alpha}$ ${\ style d'affichage A}$${\ style d'affichage B}$${\ style d'affichage A, B}$
• S'il existe un homomorphisme, les énoncés suivants sont équivalents. Dans ce cas, on parle de monomorphisme .${\ displaystyle \ alpha \ deux-points A \ à B}$${\ style d'affichage \ alpha}$

1. ${\ style d'affichage \ alpha}$ est injectif en tant qu'image.
2. ${\ displaystyle \ operatorname {core} (\ alpha) = 0}$.
3. Pour tous les groupes abéliens et tous les homomorphismes avec est . Il peut être raccourci à gauche.${\ style d'affichage C}$${\ displaystyle f, g \ deux-points C \ à A}$${\ displaystyle \ alpha \ circ f = \ alpha \ circ g}$${\ style d'affichage f = g}$${\ style d'affichage \ alpha}$

• La concaténation de monomorphismes est un monomorphisme. Cela veut dire plus précisément : Si les monomorphismes existent, alors il y a un monomorphisme.${\ displaystyle \ alpha \ deux points A \ à B, \ beta \ deux points B \ à C}$${\ displaystyle \ beta \ circ \ alpha \ deux-points A \ à C}$

Homomorphismes surjectifs

S'il existe un homomorphisme, alors les affirmations suivantes sont équivalentes. On parle alors d' épimorphisme . ${\ displaystyle \ alpha \ deux-points A \ à B}$${\ style d'affichage \ alpha}$

1. ${\ style d'affichage \ alpha}$ est surjectif comme une application.
2. ${\ style d'affichage B / \ alpha (A) = 0}$.
3. Ce qui suit s'applique à tous les groupes et à tous : Is , so is . Il peut être raccourci sur le côté droit.${\ style d'affichage C}$${\ displaystyle f, g \ deux-points B \ à C}$${\ style d'affichage f \ alpha = g \ alpha}$${\ style d'affichage f = g}$${\ style d'affichage \ alpha}$

• S'il s'agit d' un sous-groupe, la cartographie est un épimorphisme.${\ displaystyle U \ hookrightarrow A}$${\ displaystyle \ pi _ {U} \ deux-points A \ ni a \ mapsto a + U \ in A / U}$
• La concaténation d'épimorphismes est un épimorphisme. Plus précisément : si et sont des épimorphismes, alors il y a un épimorphisme. C'est ce qu'on appelle l' épimorphisme canonique .${\ displaystyle f \ deux-points A \ à B}$${\ displaystyle g \ deux points B \ à C}$${\ displaystyle g \ circ f}$
• Si et sont des homomorphismes, et s'il y a un épimorphisme, alors il y a un épimorphisme.${\ displaystyle f \ deux-points A \ à B}$${\ displaystyle g \ deux points B \ à C}$${\ displaystyle g \ circ f}$${\ style d'affichage g}$

Isomorphisme, phrases d'isomorphisme

Un homomorphisme bijectif est appelé un isomorphisme . C'est le cas si et seulement si elle est monomorphe et épimorphe. Les phrases suivantes s'appliquent. ${\ displaystyle f \ deux points A \ rightarrow B}$

• Théorème d'homomorphisme : Soit un homomorphisme. l'épimorphisme canonique. Alors il existe un monomorphisme avec . En particulier est . Le diagramme suivant est commutatif .${\ displaystyle \ alpha \ deux points A \ rightarrow B}$${\ displaystyle \ pi \ deux-points A \ rightarrow A / \ nom_opérateur {core} (\ alpha)}$${\ displaystyle \ alpha ^ {*} \ deux-points A / \ operatorname {core} (\ alpha) \ ni \ pi (a) \ mapsto \ alpha (a) \ in B}$${\ displaystyle \ alpha ^ {*} \ circ \ pi = \ alpha}$${\ displaystyle A / \ nom_opérateur {core} (\ alpha) \ cong \ alpha (A)}$
  

  Théorème de l'homomorphisme

Le théorème de l'homomorphisme s'applique généralement aux groupes.

• Premier théorème d'isomorphisme : être des sous-ensembles de . Ensuite : .${\ style d'affichage B, C}$${\ style d'affichage A}$${\ displaystyle B + C / C \ cong B / B \ cap C}$
• Second isomorphisme : être des sous-groupes. Ensuite : .${\ displaystyle C \ hookrightarrow B \ hookrightarrow A}$${\ displaystyle A / B \ cong (A / C) / (B / C)}$

Le foncteur Hom (A, -)

• S'il y a des groupes, l'ensemble est un groupe. L'ajout s'explique par : . ${\ style d'affichage A, B}$${\ displaystyle \ operatorname {Hom} (A, B) = \ {f | f \ deux-points A \ to B, \ f {\ text {est homomorphism}} \}}$${\ displaystyle (f + g) (a): = f (a) + g (a)}$
  • C'est pour tout groupe de type fini .${\ displaystyle \ operatorname {Hom} (\ mathbb {Q}, A) = 0}$${\ style d'affichage A}$
  • Est-ce que le plus grand commun diviseur de deux nombres est égal est ainsi .${\ style d'affichage a, b}$${\ style d'affichage 1}$${\ displaystyle \ operatorname {Hom} (\ mathbb {Z} / a \ mathbb {Z}, \ mathbb {Z} / b \ mathbb {Z}) = 0}$
  • Pour tous les groupes abéliens est . Cet isomorphisme est un isomorphisme fonctionnel. Ceci est expliqué plus en détail ci-dessous.${\ style d'affichage A}$${\ displaystyle A \ cong \ nom_opérateur {Hom} (\ mathbb {Z}, A)}$
• S'il s'agit d' un homomorphisme, l'affectation est un homomorphisme. Pour ce qui suit s'applique : . Si l'identité est active , alors l'identité est active . S'il y a un isomorphisme, alors c'est un isomorphisme. Devient ${\ displaystyle f \ deux-points B \ à C}$${\ displaystyle \ nom_opérateur {Hom} (A, f) \ deux-points \ nom_opérateur {Hom} (A, B) \ ni \ alpha \ mapsto f \ circ \ alpha \ in \ nom_opérateur {Hom} (A, C)}$${\ displaystyle f \ deux-points B \ à C, g \ deux-points C \ à D}$${\ displaystyle \ nom_opérateur {Hom} (A, g \ circ f) = \ nom_opérateur {Hom} (A, g) \ circ \ nom_opérateur {Hom} (A, f)}$${\ displaystyle 1_ {B}}$${\ style d'affichage B}$${\ displaystyle \ operatorname {Hom} (A, 1_ {B})}$${\ displaystyle \ operatorname {Hom} (A, B)}$${\ displaystyle f \ deux-points B \ à C}$${\ displaystyle \ nom_opérateur {Hom} (A, f) \ deux-points \ nom_opérateur {Hom} (A, B) \ à \ nom_opérateur {Hom} (A, C)}$
  • Chaque groupe abélien a le groupe abélien et${\ style d'affichage B}$${\ displaystyle \ operatorname {Hom} (A, B)}$
  • assigné l'homomorphisme à chaque homomorphisme , on obtient le foncteur de la catégorie des groupes abéliens dans la catégorie .${\ displaystyle f \ deux-points A \ à B}$${\ displaystyle \ operatorname {Hom} (A, f)}$ ${\ displaystyle \ operatorname {Hom} (A, -)}$${\ displaystyle {\ cal {A}}}$${\ displaystyle {\ cal {A}}}$
• La dernière affirmation met en lumière la propriété universelle de . Puisqu'il à chacun un homomorphisme déterminé de manière unique avec sont, l'affectation est une fonction. Ce qui suit s'applique plus précisément : La famille map : a la propriété suivante : Pour tous et tous les homomorphismes est . De plus, le mappage est un isomorphisme pour tous . La carte inverse est . C'est-à-dire que le diagramme suivant est commutatif pour tout et tout avec des isomorphismes .${\ displaystyle \ mathbb {Z}}$${\ displaystyle a \ dans A}$${\ displaystyle \ Phi _ {a} \ deux-points \ mathbb {Z} \ à A}$${\ displaystyle \ Phi _ {a} (1) = a}$${\ displaystyle \ Phi (A) \ deux-points A \ ni a \ mapsto \ Phi _ {a} \ in \ operatorname {Hom} (\ mathbb {Z}, A)}$${\ displaystyle \ {\ Phi (A) | A {\ text {groupe abélien}} \}}$${\ displaystyle A, B \ in {\ cal {A}}}$${\ displaystyle f \ deux-points A \ à B}$${\ displaystyle \ Phi (B) \ circ f = \ operatorname {Hom} (\ mathbb {Z}, f) \ circ \ Phi (A)}$${\ displaystyle A \ in {\ cal {A}}}$${\ style d'affichage \ Phi (A)}$${\ displaystyle \ Psi (A) \ colon \ operatorname {Hom} (\ mathbb {Z}, A) \ ni \ alpha \ to \ alpha (1) \ in A}$${\ displaystyle A, B \ in {\ cal {A}}}$${\ displaystyle f \ deux-points A \ à B}$${\ style d'affichage \ Phi (A), \ Phi (B)}$
  
  Cela signifie, entre autres , que le monomorphisme ou l'épimorphisme est exactement ce qu'il en est.${\ displaystyle f \ deux-points A \ à B}$${\ displaystyle \ operatorname {Hom} (\ mathbb {Z}, f)}$
• Hom (G, -) et suites exactes : Si une suite exacte est une suite exacte de groupes abéliens, alors pour chaque groupe la suite induite est exacte. C'est . Le foncteur est dit exact à gauche . S'il y a un épimorphisme, il n'y a généralement pas d'épimorphisme.${\ displaystyle 0 \ à A {\ overset {\ alpha} {\ longrightarrow}} B {\ overset {\ beta} {\ longrightarrow}} C}$${\ style d'affichage G}$${\ displaystyle 0 \ to \ operatorname {Hom} (G, A) {\ overset {\ alpha ^ {*}} {\ longrightarrow}} \ operatorname {Hom} (G, B) {\ overset {\ beta ^ { *}} {\ longrightarrow}} \ nom_opérateur {Hom} (G, C)}$${\ displaystyle \ alpha ^ {*} = \ operatorname {Hom} (G, \ alpha)}$${\ displaystyle \ operatorname {Hom} (G, -)}$${\ style d'affichage \ bêta}$${\ displaystyle \ operatorname {Hom} (G, \ beta)}$
• Les lois suivantes s'appliquent à. ${\ displaystyle \ nom_opérateur {Fin} (A): = \ nom_opérateur {Hom} (A, A)}$
  • Car tout le monde est et .${\ displaystyle f, g, h \ in \ operatorname {Fin} (A)}$${\ displaystyle f \ circ (g + h) = f \ circ g + f \ circ h}$${\ displaystyle (f + g) \ circ h = f \ circ h + g \ circ h}$
  • Car tout le monde est et .${\ displaystyle f \ in \ operatorname {Fin} (A)}$${\ displaystyle 1_ {A} \ circ f = f}$${\ displaystyle f \ circ 1_ {A} = f}$
  • Car tout le monde est . est un anneau unitaire .${\ displaystyle f, g, h \ in \ operatorname {Fin} (A)}$${\ displaystyle f \ circ (g \ circ h) = (f \ circ g) \ circ h}$${\ displaystyle \ operatorname {Fin} (A)}$

Généralisations, en cours

La théorie des groupes abéliens est riche. Certains termes de base doivent être soulignés ici. Parfois, il y a une entrée dans Wikipedia pour un aspect partiel. Surtout pas.

• Chaque module est un module au-dessus de l'anneau (voir ci - dessus ). Si nous le remplaçons par n'importe quel anneau , nous obtenons un module. Les phrases sur les groupes abéliens peuvent souvent être transférées dans des modules sur les principaux domaines idéaux . Un exemple est la classification des groupes abéliens de type fini (voir ci-dessous).${\ displaystyle \ mathbb {Z}}$${\ displaystyle \ mathbb {Z}}$ ${\ style d'affichage R}$${\ style d'affichage R}$
• Groupes de torsion : Un élément de torsion est appelé s'il existe un nombre naturel tel que . L'ensemble de tous les éléments de torsion d'un groupe forme un sous-groupe. Par exemple, le sous-groupe de torsion est de .${\ displaystyle a \ dans A}$${\ displaystyle a \ cdot n = 0}$${\ style d'affichage A}$${\ displaystyle \ mathbb {Q} / \ mathbb {Z}}$${\ displaystyle \ mathbb {R} / \ mathbb {Z}}$
• Sommes directes des groupes abéliens : Le terme est expliqué ici pour le cas de deux sous-groupes . Est et est appelée la somme directe de .${\ displaystyle U, V \ hookrightarrow A}$${\ style d'affichage A = U + V}$${\ displaystyle U \ cap V = 0}$${\ style d'affichage A}$${\ style d'affichage U, V}$
• Produit direct.
• groupe abélien libre : certains groupes abéliens ont quelque chose comme une base dans un espace vectoriel. Dans la théorie des modules, les modules libres jouent un rôle majeur.${\ style d'affichage R}$
• Groupe abélien divisible
• a finalement généré le groupe abélien . Leur structure est assez claire. Ils sont la somme directe de groupes cycliques indécomposables.
• Pour tout groupe abélien, analogue au concept de la dimension d' un espace vectoriel, chaque groupe abélien peut se voir attribuer son rang . Il est défini comme la plus grande épaisseur d' un sous-ensemble linéairement indépendant . Les entiers et les nombres rationnels sont de rang 1, comme chaque sous-groupe de . Les groupes abéliens de rang 1 sont bien compris, mais il reste encore de nombreuses questions sans réponse pour les rangs supérieurs. Les groupes abéliens de rang infini peuvent être extrêmement complexes et leurs questions ouvertes sont souvent étroitement liées à des questions de théorie des ensembles .${\ displaystyle \ mathbb {Z}}$${\ displaystyle \ mathbb {Q}}$${\ displaystyle \ mathbb {Q}}$

• De nombreux groupes abéliens ont une topologie naturelle qui en fait des groupes topologiques .

Littérature

• Siegfried Bosch : Algèbre. 7e édition revue et corrigée. Springer, Berlin et al. 2009, ISBN 978-3-540-92811-9 .
• László Fuchs : Groupes abéliens. (= Springer Monographies en Mathématiques ). Springer International, 2016, ISBN 978-3-319-19421-9 .
• Friedrich Kasch : modules et anneaux. Teubner, Stuttgart 1977, ISBN 3-519-02211-7
• Serge Lang : Algèbre (= Textes d'études supérieures en mathématiques. Volume 211). 3e, révisé. Édition. Springer, New York NY et al. 2002, ISBN 0-387-95385-X .
• Stephan Rosebrock : Théorie des groupes illustrative - une introduction géométrique orientée ordinateur. 3e édition révisée, Springer Spectrum, Berlin 2020, ISBN 978-3-662-60786-2 .

Preuve individuelle

1. ↑ Làzlò Fuchs : Groupes abéliens Springer, ISBN 978-3-319-19421-9 , p.1 .
2. ↑ Lazlo Fuchs : Groupes abéliens Springer, ISBN 978-3-319-19421-9 , page 2.
3. ↑ Làzlò Fuchs : Groupes abéliens Springer, ISBN 978-3-319-19421-9 , page 4.
4. ↑ Làzlò Fuchs : Groupes abéliens Springer, ISBN 978-3-319-19421-9 , p.3 .
5. ^ Andreas Bartholomé, Josef Rung, Hans Kern : "Théorie des nombres pour débutants" Vieweg + Teubner, 7e édition, 2010, ISBN 978-3-8348-1213-1 , page 44ff.
6. ↑ Làzlò Fuchs : Groupes abéliens Springer, ISBN 978-3-319-19421-9 , page 6.
7. ^ Friedrich Kasch : modules et anneaux. Teubner, Stuttgart 1977, page 55, ISBN 3-519-02211-7 .
8. ^ Friedrich Kasch : modules et anneaux. Teubner, Stuttgart 1977, page 57, ISBN 3-519-02211-7 .
9. ^ Friedrich Kasch : modules et anneaux. Teubner, Stuttgart 1977, page 58, ISBN 3-519-02211-7 .
10. ↑ Làzlò Fuchs : Groupes abéliens Springer, ISBN 978-3-319-19421-9 , p. 217.

liens web